Nitpicking Pick-Split

The R-tree spatial index is a translation of the B-tree index into two or more dimensions. It is amazingly powerful and also surprisingly simple. I can't do a better job of describing it than Wikipedia, so if you want some background, read there before going further.

The primary point of interest in an R-Tree algorithm is the "pick-split" function - it decides how to split up a branch in the tree that has become too full. This is where you decide whether to do it fast and dirty, or take some time to try to do a better job - the choice will effect the structure of the resulting tree, and thus the performance of searches on the tree structure. The original paper in which Antonin Guttman defined R-trees (in 1984) specified three different possible pick-split algorithms, and since then, "R-Tree have grown everywhere".

R-Tree in PostGIS are implemented using the GiST index bindings in PostgreSQL. This means that we don't have a lot of freedom to do branch-merging and other interesting and complicated R-tree optimizations - we have to work within the GiST framework (unless we want to get deeper into PostgreSQL internals to do it - which I don't, until I exhaust the other options). The pick-split function is part of the GiST concept as well - so I wonder if there is anything in there that we can do better.

The first thing I'd like to do is try to visualize the index, to see if that reveals anything - a picture is worth a thousand words. I want a picture of the guts of the index, something I'd normally consider to be deep inside PostgreSQL - lucky for me, Oleg and Teodor have just the thing - Gevel.

You'll want to view the full size image to get see the details. This isn't exactly what I was expecting to see; perhaps I should first explain exactly what it is you are looking at.

I downloaded the National Road Network shapefile for British Columbia's roads from GeoBase, and loaded it into PostGIS 1.3.3 (on PostgreSQL 8.3.4). I built an R-Tree GiST index on it, and used Gevel to inspect the index and create a new table containing the index rectangles (MBRs). You can do it too:

# createdb rtrees
# shp2pgsql -c -g geom -D -i -I NRN_BC_5_0_ROADSEG.shp nrn_roadseg | psql rtrees
# psql rtrees
# select * into nrn_roadseg_rtree from gist_print('nrn_roadseg_geom_gist') as t(level int, valid bool, bbox box2d);
# select addgeometrycolumn( '', 'nrn_roadseg_rtree', 'geom', -1, 'GEOMETRY', 2);
# update nrn_roadseg_rtree set geom = bbox;

The result of this is a table of the MBRs for all levels of the index, identified by level. I opened this table up in OpenJUMP and filtered it for level=2 to take make the image above.

I also found a place where one click could select 55 of the bounding boxes - the literature calls that the "stabbing number" (how many boxes can I stab with one pin) and the lower, the better, as far as querying performance is concerned. Another thing that concerned me was the number of long, skinny boxes, and the amount of overlap overall. But the index does work - and it seems fast - but I haven't tried comparing it against anything.

The current pick-split algorithm used in PostGIS is a linear-time approach by Ang and Tan. It is linear in the number of nodes in the branch of the tree being split; that makes it essentially minimal, there is no way you could effectively split the nodes without at least looking at each of them, or at least half of them. This time is important because it affects the amount of time it takes to insert a new record into the tree. The algorithm can't spend a lot of time deciding; what it does is to try spliting the branch in half down the center, either vertically or horizontally - it chooses the direction which is closest to splitting them in half. There are various special cases which need to be handled as well, but that is the basic idea.

It's not too hard to see that there is nothing to prevent long-skinny branches from being created. In fact, I would suggest that this algorithm, when used with varying-density data, is very likely to create long-skinny boxes. Because the data can be inserted in effectively random order, it is likely that a given box might start out including a very large area, in which there will be many boxes in the more dense areas, and fewer in the less dense areas. The ideal split will intersect the denser area - in order to evenly split the boxes, it will have to. if the dense area is not near the center of the box, one of the resultant pair of nodes will have to be significantly longer and skinnier. As more nodes are inserted, the dense area will get denser, and the same situation will occur again, creating an even longer and skinnier box. The dense areas dominate the split-decision, and the less dense areas just "come along for the ride" - turning what could have been a small squarish box in a dense area into a long, skinny box which covers a lot of features in the dense area, and a few others on the other side of the universe. This logic is totally consistent with the shape of the boxes above when compared with the varying density of the BC roads:

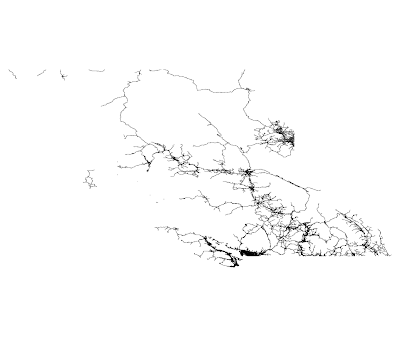Approximately one third of all the road segments in BC are in the Greater Vancouver area. I would suggest that a large portion of GIS data has similarly varying density, and I don't think that our current pick-split function is doing us any favors in dealing with it.

But in order to prove that, I'm going to need to find something better to compare against. There are two ways to go about that - improving the pick-split algorithm itself (or using a different one of the plethora that have been documented in various papers), or packing the tree. Packing is a one-time sort of operation, so you have no guarantees of what will happen to your beautiful tree if you start adding more data; but doing anything fancy in the pick-split will likely cost you extra time to do inserts. I'm going to investigate each option further - check back for more.